What is the Missing Statement in Step 4? ∠ace ≅ ∠bcd ∠eab ≅ ∠dbc ∠eac ≅ ∠eac ∠cbd ≅ ∠dbc
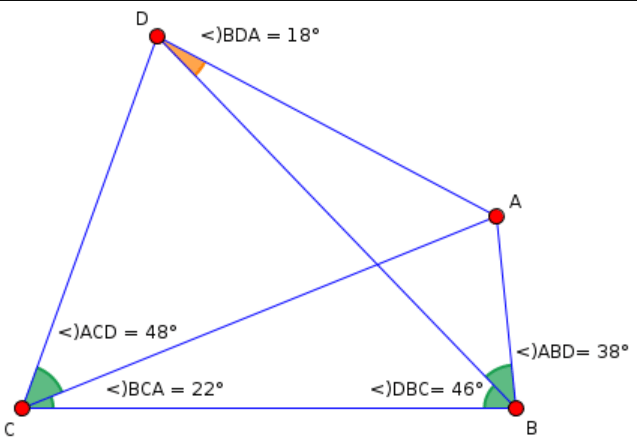
In the realm of geometry, understanding angles and their relationships is crucial. In step 4 of a geometric proof, we are presented with a series of angle pairs, and what is the missing statement in step 4? ∠ace ≅ ∠bcd ∠eab ≅ ∠dbc ∠eac ≅ ∠eac ∠cbd ≅ ∠dbcbd ≅ ∠dbc.” Let’s dive into the world of angles and proofs to uncover the missing link.
Understanding Geometry Basics
Before we delve into the missing statement, it’s essential to grasp some fundamental concepts in geometry. Geometry is the branch of mathematics that deals with the study of shapes, sizes, properties of space, and the relationships between objects. Angles are a fundamental aspect of geometry, representing the amount of rotation needed to superimpose one line or shape onto another.
What Are Congruent Angles?
When two angles are congruent, it means they are identical in terms of their size, shape, and orientation. In geometry, proving that two angles are congruent is a common task, and it relies on a set of well-defined theorems and properties.
Step 4 and the Missing Statement
Step 4 in our geometric proof presents us with a set of angle pairs and their congruence relationships. However, the statement “∠ace ≅ ∠bcd ∠eab ≅ ∠dbc ∠eac ≅ ∠eac ∠cbd ≅ ∠dbc” seems incomplete. The missing statement here is crucial to completing the proof and establishing the congruence of the angles involved.
The Importance of Congruence in Geometry
Congruence in geometry is significant because it allows us to prove that two objects or shapes are identical in size and shape. In the context of angles, congruence helps us determine whether angles are equal, which is a fundamental aspect of solving geometric problems and proofs.
Proving Congruence in Triangles
One of the common scenarios where congruence is applied is in proving that two triangles are congruent. This involves demonstrating that all corresponding sides and angles of the two triangles are equal. In the case of step 4, the missing statement is likely a key piece in proving congruence in triangles or other geometric figures.
Exploring Step 4 Further
To decipher the missing statement in step 4, we should closely examine the given information. The angles ∠ace, ∠bcd, ∠eab, ∠dbc, ∠eac, and ∠cbd all have congruence relationships, but we must figure out why.
Why ∠ace ≅ ∠bcd?
The statement ∠ace ≅ ∠bcd suggests that these two angles are congruent. This means that the angle formed between lines ac and e is equal to the angle formed between lines b, c, and d. But what connects these two angles, and why are they congruent?
Understanding ∠eab ≅ ∠dbc
The congruence between ∠eab and ∠dbc implies that these angles are identical in measurement. To understand this, we need to explore the lines and intersections that create these angles. What geometric principles connect these two angles?
Addressing ∠eac ≅ ∠eac
The statement ∠eac ≅ ∠eac may initially seem redundant, as it suggests that an angle is congruent to itself. However, it’s essential to explore why this statement is included and how it contributes to the overall proof.
The Significance of ∠cbd ≅ ∠dbc
Lastly, we encounter the statement ∠cbd ≅ ∠dbc, indicating the congruence of these two angles. It’s essential to dissect this relationship and understand the geometric logic behind it.
The Concept of Congruence in Geometry
Congruence is a fundamental concept in geometry, and understanding the missing statement in step 4 is crucial for advancing our geometric knowledge. It’s not just about proving angle congruence but also about developing problem-solving skills and critical thinking in geometry.
Applications of Congruence
Congruence extends beyond geometric proofs. It finds applications in architecture, engineering, art, and various fields where precise measurements and relationships between shapes are vital. Understanding congruence in geometry lays the foundation for practical applications in real-life scenarios.
Common Mistakes in Geometry Proofs
Geometry proofs can be challenging, and making mistakes is a common occurrence. Common errors include assuming congruence without proper proof, overlooking the significance of specific statements, and misinterpreting geometric relationships. By studying step 4 and its missing statement, we can enhance our proof-writing skills and reduce such mistakes. Read more…
Conclusion
In conclusion, the what is the missing statement in step 4? ∠ace ≅ ∠bcd ∠eab ≅ ∠dbc ∠eac ≅ ∠eac ∠cbd ≅ ∠dbc is an essential piece of the puzzle in proving the congruence of angles. It is vital to scrutinize the relationships between the given angles and lines to establish the missing link. Understanding congruence in geometry is not only a mathematical skill but also a valuable problem-solving tool.
FAQs
1. What is the significance of congruence in geometry?
Congruence is crucial in geometry as it helps us prove that two objects or angles are identical in size and shape, which is fundamental for solving geometric problems.
2. Why is it important to find the missing statement in step 4?
Finding the missing statement in step 4 is essential for completing a geometric proof and demonstrating the congruence of angles.
3. How does congruence apply to real-life scenarios?
Congruence is applied in fields like architecture, engineering, and art to ensure precise measurements and relationships between shapes.
4. What are common mistakes in geometry proofs?
Common mistakes include assuming congruence without proper proof, misinterpreting geometric relationships, and overlooking the significance of specific statements.
5. How can I improve my geometry proof-writing skills?
To improve your geometry proof-writing skills, practice analyzing geometric relationships, and study various proofs to understand the logic and steps involved.